How to square the circle with ruler and compasses only

© Stu Savory, 2005.

Please make the effort to get out your schoolday compasses and actually DO this exercise, then you'll believe me. Learn it by heart to impress your geeky friends (and/or your school's mathematics teacher), by squaring the circle !

  1. Draw a horizontal line in the middle of the paper and mark a point R at the right end.
  2. Open your compasses about an inch (roughly) and mark a point T on the line.
  3. With unchanged compasses, mark a point O on the line so that distance OT=2*TR.
  4. Draw a circle centered at O, and label point P at the left of the diameter line. This will be the circle POR whose area we are trying to equal with a square.
  5. Construct point H halfway along the line PO, (you should know how to do that).
  6. Raise a perpendicular at T, intersecting the circle at Q.
  7. Draw a chord RS of the same length as QT.
  8. Join PS and draw MO and NT both parallel to RS.
  9. Below the horizontal diameter, draw a chord PK of length PK=PM.
  10. Construct a vertical tangent PL of the same length as line segment MN.
  11. Join RL, RK and KL.
  12. Label point C on RK so that RC has length RH.
  13. Construct CD parallel to LK, meeting RL at D.
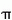  14. Construct a square on base RD. It will have the same area as the circle! You can verify this by measuring the length RD as the radius RO times the square root of (~1,7724539). So the area of the square is 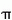*r2. Quod erat demonstrandum.

Does that knock your socks off, Euclid, or what? :-)

There is an amusing anecdote from my schooldays about this construction. We had a good maths teacher, Jeb, who often spoke ex cathedra though, that is, he didn't prove what he said. So Anthony and I set him up one day. At the start of a lesson, my good friend Anthony asked "Sir, can you show us how to go about squaring the circle?"

Jeb replied "Certainly not, boy! It is impossible to construct a square of the same area as a circle using only straightedge and compasses (Euclid's toolkit)! I told you that last lesson, pay attention!"

At this point I butted in "But you didn't prove it, sir! And you're wrong; I bet I could get the whole class to square the circle right now! Then we'll measure everyone's square and we'll see it's 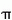*r2"

Jeb of course knew that squaring the circle is impossible, but couldn't prove it there and then. To cut a long story short, Jeb fell for it and I had the whole (unwitting) class each do the construction given above after admonishing them to go for maximum precision. Given the chance of embarrassing one of us (Jeb or cocksure me) they all made a maximally precise effort as I took them step-by-step through the construct which I had learned by rote. Everybody then measured the length of the side of their square and we averaged the result, getting ~1,7725, about the square root of 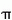. Jeb was dumbstruck, but he shook my hand and gave us the rest of the hour off, which upped my class status no end. A week later the school was still buzzing :-)

But of course, squaring the circle using only straightedge and compasses (Euclid's toolkit) IS impossible (because 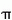is transendental {proved by Lindemann in 1882}), so what have I done? The construct actually draws a square of area (355/113)*r2 and the fraction 355/113 is an approximation to 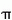which is accurate to the seventh digit. So if the pencil lead of your compass is so fine that it can draw a line only 1/100th of an inch wide, then you would need to draw a circle over 4 miles in diameter before you could notice the error. So, pure geometry apart, for all intents and engineering purposes, the construct which I showed you above DOES INDEED square the circle :-)

Of course, the construct was not mine, I was just a precocious teenager (15 or 16) then. After the previous lesson, when Jeb alleged but did not prove the impossibility, I had spent several hours in the library until finding this construct which is due to Ramanujan (originally published in the Journal of the Indian Mathematical Society, V, 1913, p132). I learned it off by heart, just to set Jeb up. Not until several weeks later did I show Jeb Ramanujan's paper. So I hope it was for some of my other maths work that they gave me the maths prize that year ;-)

But of course, if you (only just) don't restrict yourself to using compasses and straightedge ONLY, there is a much easier way to square the circle.

Assume you give me a coin (yes please) and ask me to construct a square of the same area as the coin. Just draw draw a line on the paper, and mark a point A. Draw a diameter on the coin and roll the coin along your line until the other end of the coin's diameter meets the line at point B. The length AB = 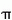r by definition. Extend the line AB to point C where BC = r = the radius of the coin. Find the centre of the line AC and draw a circle centered there so that points A and C are on a diameter of it. Now drop a vertical from point B to intersect the circle at D. Now we know that BD*BD = AB*BC = 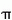r*r. So a square drawn with side BD has the same area as the circular coin. QED!
NB: I already showed you how to take square roots using only ruler and compasses.

Site Meter Now go visit my blog please, or look at other interesting maths stuff :-)

Index/Home Impressum Sitemap Search new/neu